Triangle

This article is about the basic geometric shape. For other uses, see Triangle (disambiguation).

"Triagonal" redirects here. For diagonals of three-dimensional shapes, see Space diagonal.

Triangle
A triangle
Edges and vertices	3
Schläfli symbol	{3} (for equilateral)
Area	various methods; see below

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex; the shortest segment between base and apex is the height. The area of a triangle equals one-half the product of height and base length.

In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points, when non-collinear, determine a unique triangle situated within a unique flat plane. More generally, four points in three-dimensional Euclidean space determine a tetrahedron.

In non-Euclidean geometries, three "straight" segments (having zero curvature) also determine a triangle, for instance a spherical triangle or hyperbolic triangle. A geodesic triangle is a region of a general two-dimensional surface enclosed by three sides which are straight relative to the surface (geodesics). A curvilinear triangle is a shape with three curved sides, for instance a circular triangle with circular-arc sides. This article is about straight-sided triangles in Euclidean geometry, except where otherwise noted.

Triangles are classified into different types based on their angles and the lengths of their sides. Relations between angles and side lengths are a major focus of trigonometry. In particular, the sine, cosine, and tangent functions relate side lengths and angles in right triangles.

Definition, terminology, and types

The word of triangle is the union between two words: "tri" (three) and "angle".

A triangle is a figure consisting of three line segments, each of which endpoints are connected. This forms a polygon with three sides and three angles. The terminology for categorizing triangles is more than two thousand years old, having been defined on the first page of Euclid's Elements. The names used for modern classification are either a direct transliteration of Euclid's Greek or their Latin translations.

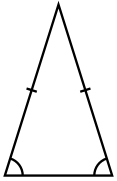
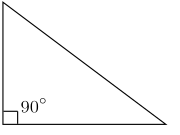
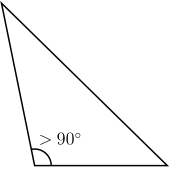
Triangles have many types based on the length of the sides and angles. In the case of the sides' length, a triangle with equal in length sides is an equilateral triangle, a triangle with two sides has the same length is an isosceles triangle, and a triangle with three different length sides is a scalene triangle. In the case of angle, a triangle in which one of the angles measuring right angle is a right triangle, a triangle in which all of its angles are less than that angle is acute angle, and a triangle in which one of it angle is greater than that angle is obtuse angle. These were defined by Ancient Greek mathematician Euclid.

• 
  Equilateral triangle
• 
  Isosceles triangle
• 
  Scalene triangle

• 
  Right triangle
• 
  Acute triangle
• 
  Obtuse triangle

Properties

Points, lines, and circles associated with a triangle

Main article: Encyclopedia of Triangle Centers

Special points associated with and often inside a triangle can be constructed differently in thousands of ways, resulting in satisfying some unique properties. They are constructed by finding three lines associated symmetrically with the three sides (or vertices) and then proving that the three lines meet in a single point. An important tool for proving the existence of these is Ceva's theorem, which gives a criterion for determining when three such lines are concurrent. Similarly, lines associated with a triangle are often constructed by proving that three symmetrically constructed points are collinear; here Menelaus' theorem gives a useful general criterion. In this section, just a few of the most commonly encountered constructions are explained.

The circumcenter is the center of a circle passing through the three vertices of the triangle; the intersection of the altitudes is the orthocenter. The intersection of the angle bisectors is the center of the incircle.

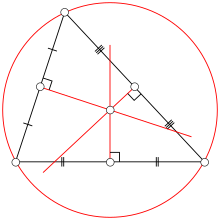
A perpendicular bisector of a side of a triangle is a straight line passing through the midpoint of the side and being perpendicular to it, forming a right angle with it. The three perpendicular bisectors meet in a single point, the triangle's circumcenter; this point is the center of the circumcircle, the circle passing through all three vertices. Thales' theorem implies that if the circumcenter is located on the side of the triangle, then the angle opposite that side is a right angle. If the circumcenter is located inside the triangle, then the triangle is acute; if the circumcenter is located outside the triangle, then the triangle is obtuse.

An altitude of a triangle is a straight line through a vertex and perpendicular to the opposite side. This opposite side is called the base of the altitude, and the point where the altitude intersects the base (or its extension) is called the foot of the altitude. The length of the altitude is the distance between the base and the vertex. The three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle is acute.

Nine-point circle demonstrates a symmetry where six points lie on the edge of the triangle. Euler's line is a straight line through the orthocenter (blue), the center of the nine-point circle (red), centroid (orange), and circumcenter (green).

An angle bisector of a triangle is a straight line through a vertex that cuts the corresponding angle in half. The three angle bisectors intersect in a single point, the incenter, the center of the triangle's incircle. The incircle is the circle that lies inside the triangle and touches all three sides. Its radius is called the inradius. There are three other important circles, the excircles; they lie outside the triangle and touch one side, as well as the extensions of the other two. The centers of the incircles and excircles form an orthocentric system. The midpoints of the three sides and the feet of the three altitudes all lie on a single circle, the triangle's nine-point circle. The remaining three points for which it is named are the midpoints of the portion of altitude between the vertices and the orthocenter. The radius of the nine-point circle is half that of the circumcircle. It touches the incircle (at the Feuerbach point) and the three excircles. The orthocenter (blue point), the center of the nine-point circle (red), the centroid (orange), and the circumcenter (green) all lie on a single line, known as Euler's line (red line). The center of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter. Generally, the incircle's center is not located on Euler's line.

The incircle of a triangle, and the intersection of the medians known as the centroid.

A median of a triangle is a straight line through a vertex and the midpoint of the opposite side, and divides the triangle into two equal areas. The three medians intersect in a single point, the triangle's centroid or geometric barycenter. The centroid of a rigid triangular object (cut out of a thin sheet of uniform density) is also its center of mass: the object can be balanced on its centroid in a uniform gravitational field. The centroid cuts every median in the ratio 2:1, i.e. the distance between a vertex and the centroid is twice the distance between the centroid and the midpoint of the opposite side. If one reflects a median in the angle bisector that passes through the same vertex, one obtains a symmedian. The three symmedians intersect in a single point, the symmedian point of the triangle.

Angles

The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal).

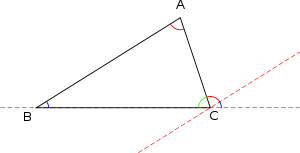
The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees. This fact is equivalent to Euclid's parallel postulate. This allows the determination of the measure of the third angle of any triangle, given the measure of two angles. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it; this is the exterior angle theorem. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees.

Another relation between the internal angles and triangles creates a new concept of trigonometric functions. The primary trigonometric functions are sine and cosine, as well as the other functions. They can be defined as the ratio between any two sides of a right triangle. In a scalene triangle, the trigonometric functions can be used to find the unknown measure of either a side or an internal angle; methods for doing so use the law of sines and the law of cosines.

Three given angles form a non-degenerate triangle (and indeed an infinitude of them) if and only if both of these conditions hold: each of the angles is positive, and the angles sum to 180°. If degenerate triangles are permitted, angles of 0° are permitted.

Three positive angles $\alpha$, $\beta$, and $\gamma$, each of them less than 180°, are the angles of a triangle if and only if any one of the following conditions holds: $${\begin{aligned}\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}+\tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}+\tan {\frac {\gamma }{2}}\tan {\frac {\alpha }{2}}&=1,\\\sin ^{2}{\frac {\alpha }{2}}+\sin ^{2}{\frac {\beta }{2}}+\sin ^{2}{\frac {\gamma }{2}}+2\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}&=1,\\\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin(\alpha )\sin(\beta )\sin(\gamma ),\\\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma +2\cos(\alpha )\cos(\beta )\cos(\gamma )&=1,\\\tan(\alpha )+\tan(\beta )+\tan(\gamma )&=\tan(\alpha )\tan(\beta )\tan(\gamma ).\end{aligned}}$$ The last equality applies only if none of the angles is 90° (so the tangent function's value is always finite).

Similarity and congruence

This diagram illustrates the geometric principle of angle-angle-side triangle congruence: given triangle ABC and triangle A'B'C', triangle ABC is congruent with triangle A'B'C' if and only if: angle CAB is congruent with angle C'A'B', and angle ABC is congruent with angle A'B'C', and BC is congruent with B'C'. Note hatch marks are used here to show angle and side equalities.

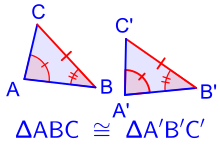
Two triangles are said to be similar, if every angle of one triangle has the same measure as the corresponding angle in the other triangle. The corresponding sides of similar triangles have lengths that are in the same proportion, and this property is also sufficient to establish similarity.

Some basic theorems about similar triangles are:

• If and only if one pair of internal angles of two triangles have the same measure as each other, and another pair also have the same measure as each other, the triangles are similar.
• If and only if one pair of corresponding sides of two triangles are in the same proportion as another pair of corresponding sides, and their included angles have the same measure, then the triangles are similar. (The included angle for any two sides of a polygon is the internal angle between those two sides.)
• If and only if three pairs of corresponding sides of two triangles are all in the same proportion, then the triangles are similar.

Two triangles that are congruent have exactly the same size and shape. All pairs of congruent triangles are also similar, but not all pairs of similar triangles are congruent. All pairs of corresponding interior angles are equal in measure, and all pairs of corresponding sides have the same length. This is a total of six equalities, but three are often sufficient to prove congruence.

Some individually necessary and sufficient conditions for a pair of triangles to be congruent are:

• SAS Postulate: Two sides in a triangle have the same length as two sides in the other triangle, and the included angles have the same measure.
• ASA: Two interior angles and the included side in a triangle have the same measure and length, respectively, as those in the other triangle. (The included side for a pair of angles is the side that is common to them.)
• SSS: Each side of a triangle has the same length as the corresponding side of the other triangle.
• AAS: Two angles and a corresponding (non-included) side in a triangle have the same measure and length, respectively, as those in the other triangle. (This is sometimes referred to as AAcorrS and then includes ASA above.)

Area

Main article: Area of a triangle

The area of a triangle can be demonstrated, for example by means of the congruence of triangles, as half of the area of a parallelogram that has the same base length and height.

Many ways to define a triangle's area. One of the simplest involves the known magnitude of the triangle's altitude and base. That being said, the area of a triangle is the half product of a base $b$ and altitude $h$: $$T={\frac {1}{2}}bh.$$ This formula may be obtained by the congruence of triangles as half of the parallelogram's area, proved and applied by both Euclid in his Elements.

Applying trigonometry to find the altitude h.

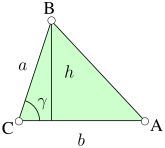
If one of the angles $\gamma$ is known using the fact that $h=a\sin(\gamma )$, as in the following image, then the area of a triangle is: $$T={\frac {1}{2}}ab\sin \gamma .$$

The Heron's formula, named after Heron of Alexandria, is a formula for finding the area of arbitrary triangles. In other words, this formula involves three sides of a triangle $a$, $b$, $c$, and its semiperimeter $s$: $$T={\sqrt {s(s-a)(s-b)(s-c)}}.$$

Inequality

Main article: Triangle inequality

The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the third side. That sum can equal the length of the third side only in the case of a degenerate triangle, one with collinear vertices. That sum cannot be less than the length of the third side. A triangle with three given positive side lengths exists if and only if those side lengths satisfy the triangle inequality.

Rigidity

Main article: Structural rigidity

Rigidity of a triangle and square

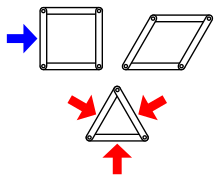
Unlike rectangle that may collapse into parallelogram from pressure to one of its point, triangles are sturdy because it has a natural strength that supports structures against lateral pressures. A triangle will not change shape unless its sides are bent or extended or broken or if its joints break; in essence, each of the three sides supports the other two. A rectangle, in contrast, is more dependent on the strength of its joints in a structural sense. Some innovative designers have proposed making bricks not out of rectangles, but with triangular shapes which can be combined in three dimensions. Triangles will be likely used increasingly in new ways as architecture increases in complexity.

Triangles are strong in terms of rigidity, but while packed in a tessellating arrangement triangles are not as strong as hexagons under compression (hence the prevalence of hexagonal forms in nature). Tessellated triangles still maintain superior strength for cantilevering however, and this is the basis for one of the strongest man-made structures, the tetrahedral truss.

Triangulation of a polygon

Main article: Polygon triangulation

Triangulation in a simple polygon

Triangulation means the partition of any planar object to be subdivided into many triangles. The polygon triangulation is an example in which the polygon can be subdivided into many triangles that are attached edge-to-edge, which has the property that their vertices coincide with the set of vertices of the polygon. In the case of simple polygon with $n$-sided, there are $n-2$ triangles and separated by $n-3$ diagonals. Triangulation of a simple polygon has a relationship to the ear, a vertex connected by two other vertices, but two of which are connected by a diagonal inside of a simple polygon forming a triangle in the end. Two ears theorem states that every simple polygon that is not itself a triangle has at least two ears.

Location of a point

One way to identify locations of points in (or outside) a triangle is to place the triangle in an arbitrary location and orientation in the Cartesian plane, and to use Cartesian coordinates. While convenient for many purposes, this approach has the disadvantage of all points' coordinate values being dependent on the arbitrary placement in the plane.

Two systems avoid that feature, so that the coordinates of a point are not affected by moving the triangle, rotating it, or reflecting it as in a mirror, any of which gives a congruent triangle, or even by rescaling it to a similar triangle:

• Trilinear coordinates specify the relative distances of a point from the sides, so that coordinates $x:y:z$ indicate that the ratio of the distance of the point from the first side to its distance from the second side is $x:y$, etc.
• Barycentric coordinates of the form $\alpha :\beta :\gamma$ specify the point's location by the relative weights that would have to be put on the three vertices in order to balance the otherwise weightless triangle on the given point.

Related figures

Figures inscribed in a triangle

As discussed above, every triangle has a unique inscribed circle (incircle) that is interior to the triangle and tangent to all three sides. Every triangle has a unique Steiner inellipse which is interior to the triangle and tangent at the midpoints of the sides. Marden's theorem shows how to find the foci of this ellipse. This ellipse has the greatest area of any ellipse tangent to all three sides of the triangle. The Mandart inellipse of a triangle is the ellipse inscribed within the triangle tangent to its sides at the contact points of its excircles. For any ellipse inscribed in a triangle $ABC$, let the foci be $P$ and $Q$, then: $${\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.$$

The pedal triangle and Gergonne triangle

From an interior point in a reference triangle, the nearest points on the three sides serve as the vertices of the pedal triangle of that point. If the interior point is the circumcenter of the reference triangle, the vertices of the pedal triangle are the midpoints of the reference triangle's sides, and so the pedal triangle is called the midpoint triangle or medial triangle. The midpoint triangle subdivides the reference triangle into four congruent triangles which are similar to the reference triangle.

The Gergonne triangle or intouch triangle of a reference triangle has its vertices at the three points of tangency of the reference triangle's sides with its incircle. The extouch triangle of a reference triangle has its vertices at the points of tangency of the reference triangle's excircles with its sides (not extended).

Every acute triangle has three inscribed squares (squares in its interior such that all four of a square's vertices lie on a side of the triangle, so two of them lie on the same side and hence one side of the square coincides with part of a side of the triangle). In a right triangle two of the squares coincide and have a vertex at the triangle's right angle, so a right triangle has only two distinct inscribed squares. An obtuse triangle has only one inscribed square, with a side coinciding with part of the triangle's longest side. Within a given triangle, a longer common side is associated with a smaller inscribed square. If an inscribed square has side of length $q_{a}$ and the triangle has a side of length $a$, part of which side coincides with a side of the square, then $q_{a}$, $a$, $h_{a}$ from the side $a$, and the triangle's area $T$ are related according to $$q_{a}={\frac {2Ta}{a^{2}+2T}}={\frac {ah_{a}}{a+h_{a}}}.$$ The largest possible ratio of the area of the inscribed square to the area of the triangle is 1/2, which occurs when $a^{2}=2T$, $q=a/2$, and the altitude of the triangle from the base of length $a$ is equal to $a$. The smallest possible ratio of the side of one inscribed square to the side of another in the same non-obtuse triangle is $2{\sqrt {2}}/3$. Both of these extreme cases occur for the isosceles right triangle.

The Lemoine hexagon inscribed in a triangle

The Lemoine hexagon is a cyclic hexagon with vertices given by the six intersections of the sides of a triangle with the three lines that are parallel to the sides and that pass through its symmedian point. In either its simple form or its self-intersecting form, the Lemoine hexagon is interior to the triangle with two vertices on each side of the triangle.

Every convex polygon with area $T$ can be inscribed in a triangle of area at most equal to $2T$. Equality holds (exclusively) for a parallelogram.

Figures circumscribed in a triangle

The circumscribed circle tangent to a triangle and the Steiner circumellipse

The tangential triangle of a reference triangle (other than a right triangle) is the triangle whose sides are on the tangent lines to the reference triangle's circumcircle at its vertices.

As mentioned above, every triangle has a unique circumcircle, a circle passing through all three vertices, whose center is the intersection of the perpendicular bisectors of the triangle's sides. Furthermore, every triangle has a unique Steiner circumellipse, which passes through the triangle's vertices and has its center at the triangle's centroid. Of all ellipses going through the triangle's vertices, it has the smallest area.

The Kiepert hyperbola is the unique conic that passes through the triangle's three vertices, its centroid, and its circumcenter.

Of all triangles contained in a given convex polygon, one with maximal area can be found in linear time; its vertices may be chosen as three of the vertices of the given polygon.

Miscellaneous triangles

Circular triangles

Main article: Circular triangle

Circular triangles with a mixture of convex and concave edges

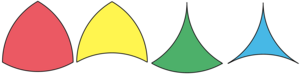
The circular triangle is a triangle with circular arc edges. The circular triangle may be shaped in the form of convexity or concavity. The circular triangles are constructed by involving the intersection of three disks. A special case of convex is Reuleaux triangle by using directly from three circles, the construction of which may be performed with a compass alone without a straightedge requirement by the Mohr–Mascheroni theorem. Alternatively, it can be constructed by rounding the sides of an equilateral triangle.

A special case of concave can be seen in a pseudo-triangle. Visually, it is the simply-connected subset of the plane in which its boundary are the curved sides. These sides are three smoothed curved lines connecting their endpoints called the cusp points. The pseudotriangle can be partitioned into many pseudotriangles with the boundaries of convex disks and bitangent lines, a process known as pseudo-triangulation. For $n$ disks in a psuedotriangle, the partition gives $2n-2$ psuedo-triangles and $3n-3$ bitangent lines. The convex hull of any pseudotriangle is triangle.

Triangle in non-planar space

Main articles: Hyperbolic triangle and Spherical triangle

Hyperbolic triangle and spherical triangle

A non-planar triangle is a triangle not included in Euclidean space, roughly speaking a flat space. This means triangles may also be discovered in several spaces, as in hyperbolic space and spherical geometry. The triangle in hyperbolic space is called hyperbolic triangle, and it can be obtained by drawing on a negatively curved surface, such as a saddle surface. The triangle in spherical geometry is called spherical triangle, and it can be obtained by drawing on a positively curved surface such as a sphere.

The triangles in both spaces have properties different from the triangles in Euclidean space. For example, as mentioned above, the internal angle's sum of a triangle in Euclidean space always equals 180°. In the case of both spaces, the internal angle's sum of a hyperbolic triangle is less than 180°, and a spherical triangle is more than 180°. and a spherical triangle. In particular, it is possible to draw a triangle on a sphere such that the measure of each of its internal angles equals to 90°, adding up to a total of 270°. Specifically, on a sphere the sum of the angles of a triangle is $180^{\circ }\times (1+4f)$, where $f$ is the fraction of the sphere's area enclosed by the triangle.

References

Works cited

• Allaire, Patricia R.; Zhou, Junmin; Yao, Haishen (2012). "Proving a nineteenth century ellipse identity"". Mathematical Gazette. 96: 161–165.
• Anglin, W. S.; Lambek, J. (1995). The Heritage of Thales. Springer. doi:10.1007/978-1-4612-0803-7. ISBN 978-1-4612-0803-7.
• Axler, Sheldon (2012). Algebra and Trigonometry. John Wiley & Sons. ISBN 978-0470-58579-5.
• Bailey, Herbert; Detemple, Duane (1998). "Squares inscribed in angles and triangles". Mathematics Magazine. 71 (4): 278–284. doi:10.1080/0025570X.1998.11996652.
• Berg, Mark Theodoor de; Kreveld, Marc van; Overmars, Mark H.; Schwarzkopf, Otfried (2000). Computational geometry: algorithms and applications (2 ed.). Berlin Heidelberg: Springer. pp. 45–61. ISBN 978-3-540-65620-3.
• Chandran, Sharat; Mount, David M. (1992). "A parallel algorithm for enclosed and enclosing triangles". International Journal of Computational Geometry & Applications. 2 (2): 191–214. doi:10.1142/S0218195992000123. MR 1168956.
• Devadoss, Satyan L.; Joseph (2011). Discrete and Computational Geometry. Princeton University Press. ISBN 978-0-691-14553-2.
• Ericson, Christer (2005). Real-Time Collision Detection. CRC Press. ISBN 978-1-55860-732-3.
• Gonick, Larry (2024). The Cartoon Guide to Geometry. William Morrow. ISBN 978-0-06-315757-6.
• Hann, Michael (2014). Structure and Form in Design: Critical Ideas for Creative Practice. A&C Black. ISBN 978-1-4725-8431-1.
• Heath, Thomas L. (1956) [1925]. The Thirteen Books of Euclid's Elements. Vol. 1 (2nd ed.). New York: Dover Publications. ISBN 0-486-60088-2.
• Holme, A. (2010). Geometry: Our Cultural Heritage. Springer. doi:10.1007/978-3-642-14441-7. ISBN 978-3-642-14441-7.
• Hungerbühler, Norbert (1994). "A short elementary proof of the Mohr-Mascheroni theorem". American Mathematical Monthly. 101 (8): 784–787. CiteSeerX 10.1.1.45.9902. doi:10.2307/2974536. JSTOR 2974536. MR 1299166.
• Jordan, D. W.; Smith, P. (2010). Mathematical Techniques: An Introduction for the Engineering, Physical, and Mathematical Sciences (4th ed.). Oxford University Press. ISBN 978-0-19-928201-2.
• Kalman, Dan (2008). "An Elementary Proof of Marden's Theorem". American Mathematical Monthly. 115: 330–338.
• King, James R. (2021). Geometry Transformed: Euclidean Plane Geometry Based on Rigid Motions. American Mathematical Society. ISBN 9781470464431.
• Lang, Serge; Murrow, Gene (1988). Geometry: A High School Course (2nd ed.). Springer. doi:10.1007/978-1-4757-2022-8. ISBN 978-1-4757-2022-8.
• Longuet-Higgins, Michael S. (2003). "On the ratio of the inradius to the circumradius of a triangle". Mathematical Gazette. 87: 119–120.
• Meisters, G. H. (1975). "Polygons have ears". The American Mathematical Monthly. 82 (6): 648–651. doi:10.2307/2319703. JSTOR 2319703. MR 0367792.
• Nielsen, Frank (2021). "On Geodesic Triangles with Right Angles in a Dually Flat Space". In Frank (ed.). Progress in Information Geometry: Theory and Applications. Springer. doi:10.1007/978-3-030-65459-7.
• Oldknow, Adrian (1995). "Computer Aided Research into Triangle Geometry". The Mathematical Gazette. 79 (485 =): 263–274. doi:10.2307/3618298. JSTOR 3618298.
• Oxman, Victor; Stupel, Moshe (2013). "Why Are the Side Lengths of the Squares Inscribed in a Triangle so Close to Each Other?". Forum Geometricorum. 13: 113–115.
• Pocchiola, Michel; Vegter, Gert (1999). "On Polygonal Covers". In Chazelle, Bernard; Goodman, Jacob E.; Pollack, Richard (eds.). Advances in Discrete and Computational Geometry: Proceedings of the 1996 AMS-IMS-SIAM Joint Summer Research Conference, Discrete and Computational Geometry—Ten Years Later, July 14-18, 1996, Mount Holyoke College.
• Ramsay, Arlan; Richtmyer, Robert D. (1995). Introduction to Hyperbolic Geometry. Springer. doi:10.1007/978-1-4757-5585-5. ISBN 978-1-4757-5585-5.
• Ryan, Mark (2008). Geometry For Dummies. John Wiley & Sons. ISBN 978-0-470-08946-0.
• Stahl, Saul (2003). Geometry from Euclid to Knots. Prentice-Hall. ISBN 0-13-032927-4.
• Usiskin, Zalman; Griffin, Jennifer (2008). The Classification of Quadrilaterals: A Study in Definition. Research in Mathematics Education. Information Age Publishing. ISBN 9781607526001.
• Vahedi, Mostafa; van der Stappen, A. Frank (2008). "Caging Polygons with Two and Three Fingers". In Akella, Srinivas; Amato, Nancy M.; Huang, Wesley; Mishra, Bud (eds.). Algorithmic Foundation of Robotics VII: Selected Contributions of the Seventh International Workshop on the Algorithmic Foundations of Robotics. doi:10.1007/978-3-540-68405-3. ISBN 978-3-540-68405-3.
• Verdiyan, Vardan; Salas, Daniel Campos (2007). "Simple trigonometric substitutions with broad results". Mathematical Reflections (6).
• Young, Cynthia (2017). Trigonometry (4th ed.). John Wiley & Sons. ISBN 978-1-119-32113-2.

External links

• Ivanov, A.B. (2001) [1994]. "Triangle". Encyclopedia of Mathematics. EMS Press.
• Clark Kimberling: Encyclopedia of triangle centers. Lists some 5200 interesting points associated with any triangle.